Topological Sort

কম্পিউটার বিজ্ঞানে টাস্ক অর্ডারিং করার জন্য টপোলজিক্যাল শর্ট অনেক জনপ্রিয়। কম্পিউটারকে যখন অনেক টাস্ক হ্যান্ডেল করতে হয়, তখন এই এলগোরিদমটি অনেক সাহায্য করে। আমাদের দৈনন্দিন জীবনেও বিভিন্ন টাস্ক অর্ডারিং করতে টপোলজিক্যাল শর্টের অনেক গুরুত্ব রয়েছে। কম্পিউটার বিজ্ঞানে তোমাকে অনেকগুলো কোর্স পড়তে হয়। তোমাকে সি, সি++, ফিজিক্স, কেমিস্ট্রি, ডাটা স্ট্রাকচার, এলগোরিদম ইত্যাদি কোর্স পড়তে হয়। এইসব সাবজেক্ট কি তোমার ইচ্ছা মতো  অর্ডারিং এ পড়তে পারো ??? যেমন আগে এলগোরিদম এরপর সি। উত্তরটি হবে না!!! সাবজেক্টগুলো একটি নির্দিষ্ট অর্ডার ফলো করে তোমাকে পড়তে হয়। কোন কোর্সের পর কোন কোর্স পড়তে হবে নিচে তার একটি তালিকা দেয়া হল।

ফিজিক্স ->সি; কেমিস্ট্রি ->সি; সি ->সি ++; সি -> এলগোরিদম; সি -> ডাটা স্ট্রাকচার; সি++ -> ডাটা স্ট্রাকচার; সি++ -> এলগোরিদম; ডাটা স্ট্রাকচার-> এলগোরিদম; 

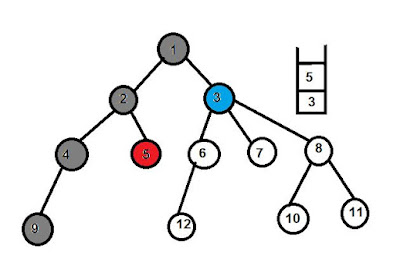
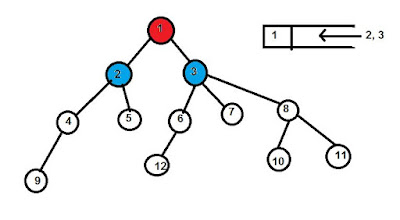
এখন প্রতিটি কোর্সকে একটি নোড হিসেবে কল্পনা করে একটি ডিরেক্টেড গ্রাফ আঁকি।

প্রতিটি কোর্স বা নোডের পাশে সংখ্যা দ্বারা ইনডিগ্রী বোঝানো হয়েছে। কোন নোডে যতটি এজ প্রবেশ করে তার সংখ্যা হিসেবে করে ইনডিগ্রী নির্ণয় করা হয়। টপোলজিক্যাল শর্ট এ যে নোডের ইনডিগ্রী জিরো সেই নোড নিয়ে অর্ডারিং শুরু করতে হয়। এখানে ফিজিক্স ও কেমিস্ট্রি দুটি নোডেরই ইনডিগ্রী শূন্য। তাই যেকোন একটি নিয়ে শুরু করতে পারি। যে নোড নিয়ে কাজ করব সেই নোড থেকে যেসব এজ বের হয়েছে সেই গুলো ডিলিট করব।

এখন মনেকর, আমরা আগে ফিজিক্স পড়ব। তাই ফিজিক্স থেকে সি এর এজটি ডিলিট করে দেই এবং সি এর ইনডিগ্রি এক কমবে।

এবার যেহেতু কেমিস্ট্রি এর ইনডিগ্রী শূন্য তাই কেমিস্ট্রি পড়ব। কেমিস্ট্রি থেকে সি এর এজটি ডিলিট করে দেই এবং সি এর ইনডিগ্রী এক কমিয়ে দেই।

এবার যেহেতু সি এর ইনডিগ্রী শূন্য তাই সি পড়ব। সি থেকে যেসব এজ বের হয়েছে সবগুলো ডিলিট করে দেই।

এবার যেহেতু সি++ এর ইনডিগ্রী শূন্য তাই সি++ পড়ব। সি++ থেকে যেসব এজ বের হয়েছে সবগুলো ডিলিট করে দেই।

এবার যেহেতু ডাটা স্ট্রাকচার এর ইনডিগ্রী শূন্য তাই ডাটা স্ট্রাকচার পড়ব। ডাটা স্ট্রাকচার থেকে যেসব এজ বের হয়েছে সবগুলো ডিলিট করে দেই।

এখন যেহেতু এলগোরিদম এর ইনডিগ্রী শূন্য তাই এলগোরিদম পড়ব। এভাবে তুমি কোর্স গুলো পড়ার অর্ডারিং পেয়ে গেছো। অর্ডারিংটি এমন- ফিজিক্স->কেমিস্ট্রি->সি->সি++ -> ডাটা স্ট্রাকচার-> এলগোরিদম। এভাবেই টপোলজিক্যাল শর্ট কাজ করে। এবার টপোলজিক্যাল শর্ট এর এলগোরিদমটি দেখ নিচে-

1. প্রথমে প্রতিটি নোডের ইনডিগ্রী নির্ণয় করতে হবে
2. যেসব নোডের ইনডিগ্রি শূন্য সেই নোড গুলোকে একটি কিউতে রাখি।
3. যতক্ষণ পর্যন্ত কিউ খালি না হয়, 4 ও 5 নম্বর ষ্টেপের জন্য লুপ চালাই
4.          কিউ থেকে ফ্রন্টের নোড N রিমুভ করি
5.          নোড N এর সাথে যুক্ত প্রতিটি নোড M এর জন্য নিচের দুটি স্টেপ রিপিট করি        

• নোড N ও নোড M এর এজ ডিলিট করি
• যেসব নোডের ইনডিগ্রী শূন্য হবে সেই গুলো কিউতে রাখি

আমরা টপোলজিক্যাল শর্ট বোঝার জন্য একটি উদাহরণ ও এলগোরিদম দেখলাম। এখন এলগোরিদমটির ইমপ্লিমেন্টেশন দেখব।

Code: 

/*  Topological Sort-Indegree  */

#include<bits/stdc++.h>
using namespace std;

vector <int> G[105];
vector <int> processed;
queue <int> q;
int indegree[105];
int n, m;

void topsort()
{
    int u;
    while(!q.empty())
    {
        u=q.front();
        q.pop();
        processed.push_back(u);
        for(int i=0; i<G[u].size(); i++)
        {
            int v=G[u][i];
            indegree[v]--;
            if(indegree[v]==0)
            {
                q.push(v);
            }
        }
    }
}

int main()
{
    int u, v;
    while(scanf("%d%d", &n, &m)==2)
    {
        if(n==0 && m==0)
            break;
        memset(indegree, 0, sizeof(indegree)); // Initialize indegree of all node to zero
        for(int i=0; i<m; i++)
        {
            scanf("%d%d", &u, &v);
            indegree[v]++;  // Increment indegree of nodes
            G[u].push_back(v);
        }

        /* Finding nodes having zero indegree and push them into queue */
        for(int i=1; i<=n; i++)
        {
            if(indegree[i]==0)
            {
                q.push(i);
            }
        }

        topsort();

        for(int i=0; i<processed.size(); i++)
        {
            printf("%d ", processed[i]);
        }
        processed.clear();
        for(int i=1; i<=n; i++)
        {
            G[i].clear();
        }
        printf("\n");
    }
    return 0;
}

টপোলজিক্যাল শর্ট রিলেটেড প্রোগ্রামিং প্রবলেমের লিংক- UVA 10305-Ordering Tasks

Kruskal Algorithm

ক্রুসকাল এলগোরিদম  দিয়ে আমরা সহজেই মিনিমাম স্প্যানিং ট্রি বের করতে পারি। ক্রুসকাল সম্পর্কে বিস্তারিত বলার আগে কিছু ডেফিনেশন জানিয়ে দেই।

একটি গ্রাফ থেকে কিছু নোড ও এজ নিয়ে আমরা সাব গ্রাফ তৈরি করতে পারি। স্প্যানিং ট্রি ও এক ধরণের সাব গ্রাফ যাতে মূল গ্রাফের সব নোড গুলো আছে কিন্তু এজ থাকবে n-1 টি যেখানে n হচ্ছে নোড সংখ্যা। একটি গ্রাফ থেকে অনেক গুলো স্প্যানিং ট্রি তৈরী করা যায়, যে স্প্যানিং ট্রি এর এজের ওয়েইটের যোগফল সর্বনিম্ন হবে তাকে  মিনিমাম স্প্যানিং ট্রি বলে। ট্রি তে সাইকেল থাকতে পারে না। 

যখন কোন গ্রাফে কোন নোড থেকে ট্রাভার্স শুরু করে বিভিন্ন এজ ট্রাভার্স করে আবার সেই নোডে ফিরে আসা যায় তাকে সাইকেল বলে।

উপরের গ্রাফটি দিয়ে ক্রুসকাল এলগোরিদম বুঝতে চেষ্টা কর। উপরের গ্রাফের এজগুলোকে প্রথমে ওয়েইট এর উপর ভিত্তি করে ছোট থেকে বড় এই অর্ডারে সাজাই। এরপর নিচের স্টেপগুলো এক্সেকিউট করব-

1. দুটি নোডের মধ্যে যে এজের ওয়েইট কম সেটি আগে নিব অর্থাৎ ওই দুটি নোড ওই এজ দ্বারা কানেক্ট করব।
2. দুটি নোডের মধ্যে যে এজের ওয়েইট বেশি সেটি পরে নিব অর্থাৎ ওই দুটি নোড ওই এজ দ্বারা কানেক্ট করব না 
3. দুটি এজের ওয়েইট সমান হলে যে কোন একটি নিব
4. এভাবে নোড গুলো কানেক্ট করার সময় যাতে সাইকেল তৈরী না হয় সেটি খেয়াল রাখতে হবে।

এখন AD ও CE দুটি এজেরই ওয়েইট সর্বনিম্ন। যেকোন একটি নেয়া যাবে। আমরা AD নিব।

 এরপর CE কে নেই

এরপর DF কে নেই

এরপর AB কে নেই

এরপর BE কে নেই

এখন BC ও EF কে নিব না কারন গ্রাফে সাইকেল তৈরি হবে। এরপর EG কে নেই

এখন BD, FG ও DE কে নিব না কারন গ্রাফে সাইকেল তৈরি হবে। এই অবস্থায় আমরা যে স্প্যানিং ট্রি টি পেলাম এটিই মিনিমাম স্প্যানিং ট্রি (MST)। 

ক্রুসকাল এলগোরিদম এর কনসেপ্ট আশা করি বুঝতে পেরেছ। আমরা যখন কোন এজ নেয়, এবং দুটি নোডের মধ্যে কানেক্ট করি, তখন ওই দুই নোডের মধ্যে পথ আছে কিনা তা জানা জরুরি। এটি আমরা ডিসজয়েন্ট সেট এলগোরিদম থেকে জানতে পারি। আমরা ক্রুসকাল এলগোরিদম এর ইম্প্লিমেন্টেশনে ডিসজয়েন্ট সেট এর কনসেপ্ট ব্যবহার করব। তাই ডিসজয়েন্ট সেট নিয়ে ইউটিউবের টিউটোরিয়ালটি আগে দেখে এসো-

Code:

/*  Kruskal */

#include <bits/stdc++.h>
using namespace std;

struct edge
{
    int u;
    int v;
    int w;
};

bool cmp(edge a, edge b)
{
    return a.w<b.w;
}

int pr[100],n,m;
edge c[100];

int find_set(int r) //parent find
{
    if(pr[r]==r)
        return r;
    else
        find_set(pr[r]);
}

int kruskal()
{
    sort(c,c+m,cmp); //sorting edges according to cost

    for(int i=1; i<=n; i++)
    {
        pr[i]=i;
    }

    int cnt=0,mst=0;

    for(int i=0; i<m && cnt<n-1; i++)
    {
        int u=find_set(c[i].u);
        int v=find_set(c[i].v);

        if(u!=v)
        {
            printf("%d %d %d\n",c[i].u, c[i].v, c[i].w);
            mst+=c[i].w;
            pr[u]=v;
            cnt++;
        }
    }
    return mst;
}

int main()
{
    scanf("%d%d", &n, &m);// n is number of nodes, m is number of edges

    for(int i=0; i<m; i++)
    {
        int u,v,w;
        scanf("%d%d%d", &u, &v, &w);
        edge input;
        input.u=u;
        input.v=v;
        input.w=w;
        c[i]=input;
    }

    printf("Minimum Spanning tree :\n");
    printf("%d", kruskal());
    return 0;
}

/*
Input:
7 11
1 2 7
1 4 5
2 3 8
2 4 9
2 5 7
3 5 5
4 5 15
4 6 6
5 6 8
5 7 9
6 7 11
*/

ক্রুসকাল এলগোরিদম রিলেটেড প্রোগ্রামিং প্রবলেম Link- UVA 11631-Dark Roads

Flood-fill Algorithm (BFS & DFS)

মনেকর, কোন প্রোগ্রামিং প্রতিযোগিতায় আমাদের সবার ফেভারিট Snake Game সম্পর্কিত একটি প্রব্লেম দেয়া হল। প্রব্লেমটিতে একটি এরিয়ার কথা বলা হয়েছে যেখানে কিছু খাবার আছে। তোমাকে সাপটি মোট কতটি খাবার খেতে পারবে তা বের করতে বলা হয়েছে। প্রব্লেমটি কিভাবে সল্ভ করবে ??? প্রব্লেমটি খুব সহজেই Flood-Fill এলগোরিদম ব্যবহার করে সল্ভ করা যায়। 

Flood-Fill এলগোরিদম যেকোন এরিয়াতে ভিজিট করতে সাহায্য করে। সাধারণত উল্লেখিত এরিয়াটি মূলত একটি ম্যাট্রিক্স যাতে প্রতিটি সেল একে-অপরের সাথে যুক্ত। Multi Dimensional Array দিয়ে তুমি এই ম্যাট্রিক্সটি সহজেই বানাতে পারো। তোমরা গ্রাফের টিউটোরিয়ালে নোড ও এজ সম্পর্কে ধারণা পেয়েছো। এখানে প্রতিটি সেলকে গ্রাফের নোড হিসেবে বিবেচনা করলে Flood-Fill এলগোরিদম তোমার জন্য সহজ হয়ে যাবে। 

এখন একটি ম্যাট্রিক্স কল্পনা করো যার যে কোন একটি সেল (x,y) এর কো-অর্ডিনেট (0,0) হলে, সেই সেল থেকে চার দিকে অর্থাৎ উপরে-নিচে, ডানে-বামে আমরা (x-1, y), (x+1, y), (x, y+1) ও  (x, y-1) এই সেলগুলোতে যেতে পারব কারণ এই সেলগুলো (x,y) এর সাথে যুক্ত।

একইভাবে আমরা যদি আট দিকে অর্থাৎ সব ডিরেকশনে যেতে চাই তাহলে সেল (x,y) থেকে (x-1, y-1), (x-1, y), (x-1, y+1), (x, y-1), (x, y+1), (x+1, y-1), (x+1, y) ও (x+1, y+1) এই সেলগুলোতে যেতে পারব।

এখন প্রোগ্রামিং প্রবলেম রিলেটেড কথায় আসি। মনেকর, Snake Games রিলেটেড একটি প্রব্লেমে তোমাকে একটি ম্যাটিক্স দেয়া হলো, তোমাকে সাপটির Starting সেল বলে দেয়া হল এবং সাপটি কতটি খাবার খেতে পারে তা বের করতে বলা হল। এখন প্রতিটি সেলকে নোড হিসেবে বিবেচনা কর। আমরা ডিএফএস এলগোরিদম থেকে তা জেনেছি যে - যেকোন নোডের সাথে যুক্ত প্রতিটি নোডে ট্রাভার্স করা যায়। এভাবে আমরা ডিএফএস এলগোরিদম ব্যবহার করে Starting সেলের বা নোডের সাথে যুক্ত সব সেলে বা  নোডে ট্রাভার্স করবো এবং কোনো নোডে খাবার পেলে তা কাউন্ট করব। অনেক সহজ না ???? নিচে Flood-Fill এর জন্য ডিএফএস এর কোড দেয়া হল-

Code:

/* DFS-Maze */

#include<bits/stdc++.h>
using namespace std;
int xx[]= {1,-1,0,0}; //For 4 direction
int yy[]= {0,0,1,-1};  // For 4 directions
/*int xx[]= {0,0,1,1,-1,-1,1,-1}; //For 8 direction
int yy[]= {1,-1,1,-1,1,-1,0,0}; // For 8 direction*/
char s[105][105];
bool visit[105][105];
long long int sx,sy,r,c;

bool dfs(long long int ux,long long int uy)
{
    bool ret=0;
    if(s[ux][uy]=='D')
    {
        return 1; //destination found
    }
    for(int i=0; i<4; i++)
    {
        int vx=ux+xx[i];
        int vy=uy+yy[i];

        if(vx<0 || vy<0 || vx>=r || vy>=c)
            continue;

        if(visit[vx][vy]==1 || s[vx][vy]=='#')
            continue;

        visit[vx][vy]=1;
        ret = ret || dfs(vx,vy);
    }
    return ret;
}


int main()
{
    long long int i,j,k;
    scanf("%lld%lld", &r, &c);
    for(i=0; i<r; i++)
    {
        scanf("%s",s[i]);
        for(j=0; j<c; j++)
        {
            if(s[i][j]=='S')
            {
                sx=i;
                sy=j;
            }
        }
    }
    visit[sx][sy]=1;
    if(dfs(sx,sy)==1)
    {
        printf("yes");
    }
    else
    {
        printf("no");
    }
    return 0;
}

/*
Input:
3 4
S.#.
.#D.
....
*/

এবার আরেকটি প্রোগ্রামিং প্রব্লেম রিলেটেড আলোচনায় আসি। মনেকর, দিপু বিশ্ববিদ্যালয় থেকে বাড়ি যাবে। তোমাকে একটি ম্যাট্রিক্স দেয়া হল যাতে দিপুর বিশ্ববিদ্যালয়ের লোকেশন নোড দেয়া আছে এবং তার বাড়ির লোকেশন নোড দেয়া আছে। তার বিশ্ববিদ্যালয় থেকে বাড়ি যাওয়ার অনেক  গুলো পথ আছে। অল্প সময়ে দিপু কত দূরত্ব অতিক্রম করে বাড়ি পৌঁছাতে পারে তা বের করতে বলা হলো তোমাকে। তুমি কিভাবে করবে??? তোমাকে বলা হয়েছে নূন্যতম দূরত্ব বা শর্টেস্ট পাথ বের করতে। যে কোন নোড থেকে অন্য যেকোন নোডের শর্টেস্ট পাথ বের করার পদ্ধতি আমরা বিএফএস এলগোরিদম থেকে জেনেছি। এভাবে বিএফএস এলগোরিদম ব্যবহার করে যেকোন ম্যাট্রিক্সে শর্টেস্ট পাথ খুব সহজেই বের করা যায়। নিচে Flood-Fill এর জন্য বিএফএস এর কোড দেয়া হল-

Code:

/* BFS-Maze */

#include<bits/stdc++.h>
using namespace std;
int xx[]= {1,-1,0,0}; //For 4 direction
int yy[]= {0,0,1,-1};  // For 4 directions
/*int xx[]= {0,0,1,1,-1,-1,1,-1}; //For 8 direction
int yy[]= {1,-1,1,-1,1,-1,0,0}; // For 8 direction*/
char s[105][105];
bool visit[105][105];
int dis[100][100];
long long int sx,sy,r,c;
queue <long long int> q1;
queue <long long int> q2;
int bfs(long long int ux,long long int uy)
{
    long long int ux1, uy1, vx1, vy1;
    q1.push(ux);
    q2.push(uy);
    visit[ux][uy]=1;
    while(!q1.empty() && !q2.empty())
    {
        ux1=q1.front();
        uy1=q2.front();
        q1.pop();
        q2.pop();
        if(s[ux1][uy1]=='D')
        {
            return dis[ux1][uy1]; //destination found
        }
        for(int i=0; i<4; i++)
        {
            int vx=ux1+xx[i];
            int vy=uy1+yy[i];
            if(vx<0 || vy<0 || vx>=r || vy>=c)
                continue;

            if(visit[vx][vy]==1 || s[vx][vy]=='#')
                continue;

            visit[vx][vy]=1;
            q1.push(vx);
            q2.push(vy);
            dis[vx][vy]=dis[ux1][uy1]+1;
        }
    }
}


int main()
{
    long long int i, j, d1;
    scanf("%lld%lld", &r, &c);
    for(i=0; i<r; i++)
    {
        scanf("%s",s[i]);
        for(j=0; j<c; j++)
        {
            if(s[i][j]=='S')
            {
                sx=i;
                sy=j;
            }
        }
    }
    d1=bfs(sx, sy);
    printf("%lld", d1);
    return 0;
}

প্রোগ্রামিং প্রবলেম : 

LightOJ 1238-Power Puff Girls

LightOJ 1012-Guilty Prince 

LightOJ 1337-The Crystal Maze 

UVA 352-Seasonal War

UVA 469-Wetlands of Florida

DFS (Depth-First Search)

গ্রাফে ট্রাভার্সিং এর অপর একটি জনপ্রিয় এলগোরিদম ডিএফএস । ডিএফএস জানার আগে বিএফএস এর টিউটোরিয়ালটি দেখে এসো - BFS Tutorial Link
বিএফএস এলগোরিদমের সাথে ডিএফএস এর অনেক সাদৃশ্য আছে। বিএফএস এ আমরা শর্টেস্ট পাথ বের করতাম। ডিএফএস এ আমরা যেকোন একটি নোড থেকে যেসব নোডে ট্রাভার্স করা যায় তা বের  করব। ডিএফএস ইমপ্লিমেন্ট করা হয় স্ট্যাক ব্যবহার করে। আমরা জানি যে স্ট্যাক লাস্ট ইন ফার্স্ট আউট মেথডলজিতে এক্সেকিউশন করে। আমরা ডিএফএস এর জন্য রিকার্শন ব্যবহার করে স্ট্যাক এর ডাটা স্ট্রাকচার ইমপ্লিমেন্ট করব। ডিএফএস এর এলগোরিদমটি  এমন -

• সব নোড গুলো প্রথমে Ready স্টেট এ থাকবে (সাদা রং দিয়ে চিহ্নিত) 
• Starting Node কে স্ট্যাকে পুশ করি এবং নোডটির Status Waiting State এ পরিবর্তন করি
• যতক্ষণ স্ট্যাক খালি না হয়, পরবর্তী দুইটি ধাপের জন্য লুপ চালাই

1. স্ট্যাক এর টপ এর ডাটা পপ করি বা রিমুভ করি এবং নোডটির রং পরিবর্তন করে গ্রে করি   
2. পপকৃত নোডটির Neighbor নোড গুলো কে স্ট্যাকে পুশ করি  এবং নোডটির Status Waiting State এ পরিবর্তন করি (নীল রং দ্বারা নির্দেশিত)

উপরের গ্রাফটি লক্ষ্য কর।এখন মনেকর, আমি নোড 1 থেকে যেসব নোডে যাওয়া যায় তা বের করব। যে নোড নিয়ে প্রথমে ট্রাভার্স শুরু করব, সেটি লাল রং দিয়ে চিহ্নিত করি, এবং সেই নোডের Neighbor নোডগুলোকে নীল রং দিয়ে চিহ্নিত করি। যেসব নোড ভিজিটেড হয়ে যাবে সেইগুলো গ্রে রং দিয়ে চিহ্নিত করি।

প্রথমে নোড 1 কে স্ট্যাকে পুশ করি। যেহেতু নোড 1 স্ট্যাকে টপে আছে সেহেতু নোড 1 কে স্ট্যাক থেকে পপ করি, নোড 1 কে  গ্রে রং দিয়ে চিহ্নিত করি এবং নোড 1 এর Neighbor নোডগুলোকে স্ট্যাকে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1।

এখন স্ট্যাকে টপে 2 আছে। 2 কে পপ করি এবং এর Neighbor নোডগুলোকে স্ট্যাকে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2

এখন স্ট্যাকে টপে 4 আছে। 4 কে পপ করি এবং এর Neighbor নোডগুলোকে স্ট্যাকে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 4

এখন স্ট্যাকে টপে 9 আছে। 9 কে পপ করি এবং নোড 9 এর Neighbor নোড না থাকায় স্ট্যাকে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ- 1, 2, 4, 9

এখন স্ট্যাকে টপে 5 আছে। 5 কে পপ করি এবং নোড 5 এর Neighbor নোড না থাকায় স্ট্যাকে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ- 1, 2, 4, 9, 5

এখন স্ট্যাকে টপে 3 আছে। 3 কে পপ করি এবং এর Neighbor নোডগুলোকে স্ট্যাকে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 4, 9, 5, 3

এখন স্ট্যাকে টপে 6 আছে। 6 কে পপ করি এবং এর Neighbor নোডগুলোকে স্ট্যাকে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 4, 9, 5, 3, 6

এখন স্ট্যাকে টপে 12 আছে। 12 কে পপ করি এবং নোড 12 এর Neighbor নোড না থাকায় স্ট্যাকে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-1, 2, 4, 9, 5, 3, 6, 12 । একইভাবে নোড 7 এর এর Neighbor নোড না থাকায় স্ট্যাকে কিছু পুশ করবো না। নোড 7 কে ভিজিট করার পর ভিজিটেড নোড সমূহ-1, 2, 4, 9, 5, 3, 6, 12, 7

এখন স্ট্যাকে টপে 8 আছে। 8 কে পপ করি এবং এর Neighbor নোডগুলোকে স্ট্যাকে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 4, 9, 5, 3, 6, 12, 7, 8

এখন স্ট্যাকে টপে 10 আছে। 10 কে পপ করি এবং এবং নোড 10 এর Neighbor নোড না থাকায় স্ট্যাকে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ- 1, 2, 4, 9, 5, 3, 6, 12, 7, 8, 10 । একইভাবে নোড 11 এর এর Neighbor নোড না থাকায় স্ট্যাকে কিছু পুশ করবো না। নোড 11 কে ভিজিট করার পর ভিজিটেড নোড সমূহ-1, 2, 4, 9, 5, 3, 6, 12, 7, 8, 10, 11

নোড 11 কে ভিজিট করার পর, স্ট্যাক সম্পূর্ণ খালি হয়ে গেছে। ভিজিটেড নোড গুলোই হচ্ছে স্টার্টিং নোড 1 থেকে Reachable । তোমরা একটি ব্যাপার কি লক্ষ্য করেছ ??? ডিএফএস এলগোরিদমের সাথে বাইনারি ট্রি এর In Order Traversal এর অনেক সাদৃশ্য আছে। 

Code:

/* DFS */

#include<bits/stdc++.h>
using namespace std;
vector <int> G[100];
bool visit[100]={0};

void dfs(int u)
{
    printf("%d ", u);
    for(int i=0; i<G[u].size(); i++)
    {
        int v=G[u][i];
        if(visit[v]==0)
        {
            visit[v]=1;
            dfs(v);
        }
    }
}


int main()
{
    int n, m, u, v, u1, v1;
    scanf("%d%d", &n, &m);  //n is number of node & m is number of edge
    for(int i=0; i<m; i++)
    {
        scanf("%d%d", &u, &v);  //u and v are two two node of an edge
        G[u].push_back(v);
        G[v].push_back(u); // For bidirectional edge
    }
    visit[1]=1;
    dfs(1);
    return 0;
}

/*
Input:
12 11
1 2
1 3
2 4
2 5
3 6
3 7
3 8
4 9
6 12
8 10
8 11
*/

BFS (Breadth-First Search)

গ্রাফে ট্রাভার্সিং এর জন্য বিএফএস খুব জনপ্রিয় এলগোরিদম। বিএফএস এর মাধ্যমে আমরা কোন গ্রাফে এক নোড থেকে অন্য নোডে যাওয়ার শর্টেস্ট পাথ বের করতে পারি। তোমরা বিএফএস সম্পর্কে অনেক কন্সেপচুয়াল তথ্য জানো, তাই আমি সেই পথে যাচ্ছি না। সাধারণত বিএফএস ইমপ্লিমেন্ট করা হয় কিউ এর মাধ্যমে। বিএফএস এর এলগোরিদমটি  এমন -

•         সব নোড গুলো প্রথমে Ready স্টেট এ থাকবে (সাদা রং দিয়ে চিহ্নিত) 
•         Starting Node কে কিউতে পুশ করি এবং নোডটির Status Waiting State এ পরিবর্তন করি
•    যতক্ষণ কিউ খালি না হয়, পরবর্তী দুইটি ধাপের জন্য লুপ চালাই
  
  • কিউ এর ফ্রন্ট এর ডাটা পপ করি বা রিমুভ করি এবং নোডটির রং পরিবর্তন করে গ্রে করি 
  • পপকৃত নোডটির Neighbor নোড গুলো কে কিউতে পুশ করি  এবং নোডটির Status Waiting State এ পরিবর্তন করি (নীল রং দ্বারা নির্দেশিত) 

উপরের গ্রাফটি লক্ষ্য কর।এখন মনেকর, আমি নোড 1 থেকে নোড 10 এর মধ্যে বিএফএস এর মাধ্যমে শর্টেস্ট পাথ বের করব। যে নোড নিয়ে প্রথমে ট্রাভার্স শুরু করব, সেটি লাল রং দিয়ে চিহ্নিত করি, এবং সেই নোডের Neighbor নোডগুলোকে নীল রং দিয়ে চিহ্নিত করি। যেসব নোড ভিজিটেড হয়ে যাবে সেইগুলো গ্রে রং দিয়ে চিহ্নিত করি।

নোড 1 ভিজিটেড হয়ে যাওয়ার পর নোড 1 কে কিউ থেকে পপ করি, নোড 1 কে  গ্রে রং দিয়ে চিহ্নিত করি এবং নোড 1 এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1। আমরা নোড 1 থেকে নোড 10 পর্যন্ত শর্টেস্ট পাথ বের করছি তাই যতক্ষণ পর্যন্ত নোড 10 ভিজিট করা হবে না ততক্ষন পর্যন্ত এই প্রক্রিয়া চলবে।

এখন কিউ এর ফ্রন্টে 2 আছে। 2 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2

এখন কিউ এর ফ্রন্টে 3 আছে। 3 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3

এখন কিউ এর ফ্রন্টে 4 আছে। 4 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি।Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4

এখন কিউ এর ফ্রন্টে 5 আছে। 5 কে পপ করি এবং 5 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5

এখন কিউ এর ফ্রন্টে 6 আছে। 6 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5, 6

এখন কিউ এর ফ্রন্টে 7 আছে। 7 কে পপ করি এবং 7 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-  1, 2, 3, 4, 5, 6, 7

এখন কিউ এর ফ্রন্টে 8 আছে। 8 কে পপ করি এবং এর  Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5, 6, 7, 8

এভাবে 9 ও 12 কে পপ করি এবং 9 ও 12 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-  1, 2, 3, 4, 5, 6, 7, 8, 9, 12 । এখন কিউ এর ফ্রন্টে 10 আছে। 10 কে পপ করি । যেহেতু নোড  10 ভিজিটেড হয়ে গেছে সেহেতু ট্রাভার্সিং প্রক্রিয়া এখানে বন্ধ করি। 

এবার নোড ১ থেকে ১০ পর্যন্ত পাথের দূরত্ব নির্ণয় করি। পাথের দূরত্ব নির্ণয়ের পদ্ধতিটি একদম সহজ। আমরা যে নোডে ভিজিট করব সেই নোডের সাথে প্যারেন্ট নোডের ডিস্টেন্স 1 হবে। যেমন আমরা সর্বশেষ নোড 10 ভিজিট করেছি। নোড 10 থেকে এবার ব্যাক-ট্র্যাকিং করব নোড 1 পর্যন্ত। নোড 10 এর প্যারেন্ট নোড 8; নোড 10 থেকে নোড 8 এর ডিসটেন্স 1 । নোড 8 এর প্যারেন্ট নোড 3; নোড 8 থেকে নোড 3 এর ডিসটেন্স 1 । নোড 3 এর প্যারেন্ট নোড 1; নোড 3 থেকে নোড 1 এর ডিসটেন্স 1 ।  নোড ১ থেকে ১০ পর্যন্ত পাথের সর্বমোট দূরত্ব 3 ।

Code:

/*  BFS */

#include<bits/stdc++.h>
using namespace std;
vector <int> G[100];
bool visit[100]= {0};
int dis[100]={0};
queue <int> q;


int bfs(int s, int d)
{
    int u, v;
    q.push(s);
    visit[s]=1;
    while(!q.empty())
    {
        u=q.front();
        printf("%d ", u);
        q.pop();
        if(u==d)
        {
            return dis[u];
        }
        for(int i=0; i<G[u].size(); i++)
        {
            int v=G[u][i];
            if(visit[v]==0)
            {
                visit[v]=1;
                q.push(v);
                dis[v]=dis[u]+1;
            }
        }
    }
}


int main()
{
    int n, m, u, v, s, d, d1;
    scanf("%d%d", &n, &m);  //n is number of node & m is number of edge
    for(int i=0; i<m; i++)
    {
        scanf("%d%d", &u, &v);  //u and v are two two node of an edge
        G[u].push_back(v);
        G[v].push_back(u); // For bidirectional edge
    }
    printf("S=");
    scanf("%d", &s);
    printf("D=");
    scanf("%d", &d);
    d1=bfs(s, d);
    printf("\n%d", d1);
    return 0;
}

/*
Input:

12 11
1 2
1 3
2 4
2 5
3 6
3 7
3 8
4 9
6 12
8 10
8 11
*/