BFS (Breadth-First Search)

গ্রাফে ট্রাভার্সিং এর জন্য বিএফএস খুব জনপ্রিয় এলগোরিদম। বিএফএস এর মাধ্যমে আমরা কোন গ্রাফে এক নোড থেকে অন্য নোডে যাওয়ার শর্টেস্ট পাথ বের করতে পারি। তোমরা বিএফএস সম্পর্কে অনেক কন্সেপচুয়াল তথ্য জানো, তাই আমি সেই পথে যাচ্ছি না। সাধারণত বিএফএস ইমপ্লিমেন্ট করা হয় কিউ এর মাধ্যমে। বিএফএস এর এলগোরিদমটি  এমন -

•         সব নোড গুলো প্রথমে Ready স্টেট এ থাকবে (সাদা রং দিয়ে চিহ্নিত) 
•         Starting Node কে কিউতে পুশ করি এবং নোডটির Status Waiting State এ পরিবর্তন করি
•    যতক্ষণ কিউ খালি না হয়, পরবর্তী দুইটি ধাপের জন্য লুপ চালাই
  
  • কিউ এর ফ্রন্ট এর ডাটা পপ করি বা রিমুভ করি এবং নোডটির রং পরিবর্তন করে গ্রে করি 
  • পপকৃত নোডটির Neighbor নোড গুলো কে কিউতে পুশ করি  এবং নোডটির Status Waiting State এ পরিবর্তন করি (নীল রং দ্বারা নির্দেশিত) 

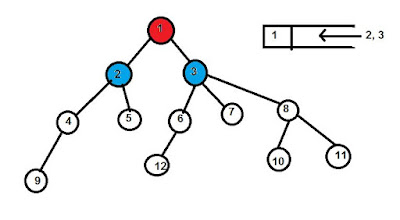
উপরের গ্রাফটি লক্ষ্য কর।এখন মনেকর, আমি নোড 1 থেকে নোড 10 এর মধ্যে বিএফএস এর মাধ্যমে শর্টেস্ট পাথ বের করব। যে নোড নিয়ে প্রথমে ট্রাভার্স শুরু করব, সেটি লাল রং দিয়ে চিহ্নিত করি, এবং সেই নোডের Neighbor নোডগুলোকে নীল রং দিয়ে চিহ্নিত করি। যেসব নোড ভিজিটেড হয়ে যাবে সেইগুলো গ্রে রং দিয়ে চিহ্নিত করি।

নোড 1 ভিজিটেড হয়ে যাওয়ার পর নোড 1 কে কিউ থেকে পপ করি, নোড 1 কে  গ্রে রং দিয়ে চিহ্নিত করি এবং নোড 1 এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1। আমরা নোড 1 থেকে নোড 10 পর্যন্ত শর্টেস্ট পাথ বের করছি তাই যতক্ষণ পর্যন্ত নোড 10 ভিজিট করা হবে না ততক্ষন পর্যন্ত এই প্রক্রিয়া চলবে।

এখন কিউ এর ফ্রন্টে 2 আছে। 2 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2

এখন কিউ এর ফ্রন্টে 3 আছে। 3 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3

এখন কিউ এর ফ্রন্টে 4 আছে। 4 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি।Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4

এখন কিউ এর ফ্রন্টে 5 আছে। 5 কে পপ করি এবং 5 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5

এখন কিউ এর ফ্রন্টে 6 আছে। 6 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5, 6

এখন কিউ এর ফ্রন্টে 7 আছে। 7 কে পপ করি এবং 7 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-  1, 2, 3, 4, 5, 6, 7

এখন কিউ এর ফ্রন্টে 8 আছে। 8 কে পপ করি এবং এর  Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5, 6, 7, 8

এভাবে 9 ও 12 কে পপ করি এবং 9 ও 12 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-  1, 2, 3, 4, 5, 6, 7, 8, 9, 12 । এখন কিউ এর ফ্রন্টে 10 আছে। 10 কে পপ করি । যেহেতু নোড  10 ভিজিটেড হয়ে গেছে সেহেতু ট্রাভার্সিং প্রক্রিয়া এখানে বন্ধ করি। 

এবার নোড ১ থেকে ১০ পর্যন্ত পাথের দূরত্ব নির্ণয় করি। পাথের দূরত্ব নির্ণয়ের পদ্ধতিটি একদম সহজ। আমরা যে নোডে ভিজিট করব সেই নোডের সাথে প্যারেন্ট নোডের ডিস্টেন্স 1 হবে। যেমন আমরা সর্বশেষ নোড 10 ভিজিট করেছি। নোড 10 থেকে এবার ব্যাক-ট্র্যাকিং করব নোড 1 পর্যন্ত। নোড 10 এর প্যারেন্ট নোড 8; নোড 10 থেকে নোড 8 এর ডিসটেন্স 1 । নোড 8 এর প্যারেন্ট নোড 3; নোড 8 থেকে নোড 3 এর ডিসটেন্স 1 । নোড 3 এর প্যারেন্ট নোড 1; নোড 3 থেকে নোড 1 এর ডিসটেন্স 1 ।  নোড ১ থেকে ১০ পর্যন্ত পাথের সর্বমোট দূরত্ব 3 ।

Code:

/*  BFS */

#include<bits/stdc++.h>
using namespace std;
vector <int> G[100];
bool visit[100]= {0};
int dis[100]={0};
queue <int> q;


int bfs(int s, int d)
{
    int u, v;
    q.push(s);
    visit[s]=1;
    while(!q.empty())
    {
        u=q.front();
        printf("%d ", u);
        q.pop();
        if(u==d)
        {
            return dis[u];
        }
        for(int i=0; i<G[u].size(); i++)
        {
            int v=G[u][i];
            if(visit[v]==0)
            {
                visit[v]=1;
                q.push(v);
                dis[v]=dis[u]+1;
            }
        }
    }
}


int main()
{
    int n, m, u, v, s, d, d1;
    scanf("%d%d", &n, &m);  //n is number of node & m is number of edge
    for(int i=0; i<m; i++)
    {
        scanf("%d%d", &u, &v);  //u and v are two two node of an edge
        G[u].push_back(v);
        G[v].push_back(u); // For bidirectional edge
    }
    printf("S=");
    scanf("%d", &s);
    printf("D=");
    scanf("%d", &d);
    d1=bfs(s, d);
    printf("\n%d", d1);
    return 0;
}

/*
Input:

12 11
1 2
1 3
2 4
2 5
3 6
3 7
3 8
4 9
6 12
8 10
8 11
*/