BFS (Breadth-First Search)

গ্রাফে ট্রাভার্সিং এর জন্য বিএফএস খুব জনপ্রিয় এলগোরিদম। বিএফএস এর মাধ্যমে আমরা কোন গ্রাফে এক নোড থেকে অন্য নোডে যাওয়ার শর্টেস্ট পাথ বের করতে পারি। তোমরা বিএফএস সম্পর্কে অনেক কন্সেপচুয়াল তথ্য জানো, তাই আমি সেই পথে যাচ্ছি না। সাধারণত বিএফএস ইমপ্লিমেন্ট করা হয় কিউ এর মাধ্যমে। বিএফএস এর এলগোরিদমটি  এমন -

•         সব নোড গুলো প্রথমে Ready স্টেট এ থাকবে (সাদা রং দিয়ে চিহ্নিত) 
•         Starting Node কে কিউতে পুশ করি এবং নোডটির Status Waiting State এ পরিবর্তন করি
•    যতক্ষণ কিউ খালি না হয়, পরবর্তী দুইটি ধাপের জন্য লুপ চালাই
  
  • কিউ এর ফ্রন্ট এর ডাটা পপ করি বা রিমুভ করি এবং নোডটির রং পরিবর্তন করে গ্রে করি 
  • পপকৃত নোডটির Neighbor নোড গুলো কে কিউতে পুশ করি  এবং নোডটির Status Waiting State এ পরিবর্তন করি (নীল রং দ্বারা নির্দেশিত) 

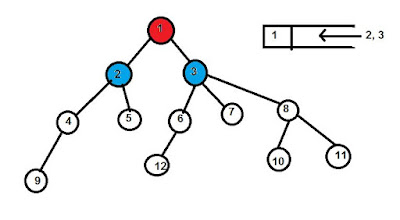
উপরের গ্রাফটি লক্ষ্য কর।এখন মনেকর, আমি নোড 1 থেকে নোড 10 এর মধ্যে বিএফএস এর মাধ্যমে শর্টেস্ট পাথ বের করব। যে নোড নিয়ে প্রথমে ট্রাভার্স শুরু করব, সেটি লাল রং দিয়ে চিহ্নিত করি, এবং সেই নোডের Neighbor নোডগুলোকে নীল রং দিয়ে চিহ্নিত করি। যেসব নোড ভিজিটেড হয়ে যাবে সেইগুলো গ্রে রং দিয়ে চিহ্নিত করি।

নোড 1 ভিজিটেড হয়ে যাওয়ার পর নোড 1 কে কিউ থেকে পপ করি, নোড 1 কে  গ্রে রং দিয়ে চিহ্নিত করি এবং নোড 1 এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1। আমরা নোড 1 থেকে নোড 10 পর্যন্ত শর্টেস্ট পাথ বের করছি তাই যতক্ষণ পর্যন্ত নোড 10 ভিজিট করা হবে না ততক্ষন পর্যন্ত এই প্রক্রিয়া চলবে।

এখন কিউ এর ফ্রন্টে 2 আছে। 2 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2

এখন কিউ এর ফ্রন্টে 3 আছে। 3 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3

এখন কিউ এর ফ্রন্টে 4 আছে। 4 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি।Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4

এখন কিউ এর ফ্রন্টে 5 আছে। 5 কে পপ করি এবং 5 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5

এখন কিউ এর ফ্রন্টে 6 আছে। 6 কে পপ করি এবং এর Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5, 6

এখন কিউ এর ফ্রন্টে 7 আছে। 7 কে পপ করি এবং 7 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-  1, 2, 3, 4, 5, 6, 7

এখন কিউ এর ফ্রন্টে 8 আছে। 8 কে পপ করি এবং এর  Neighbor নোডগুলোকে কিউতে পুশ করি। Neighbor নোডগুলোকে  নীল রং দিয়ে চিহ্নিত করি। ভিজিটেড নোড সমূহ- 1, 2, 3, 4, 5, 6, 7, 8

এভাবে 9 ও 12 কে পপ করি এবং 9 ও 12 এর কোন Neighbor নোড না থাকায় কিউতে কিছু পুশ করবো না। ভিজিটেড নোড সমূহ-  1, 2, 3, 4, 5, 6, 7, 8, 9, 12 । এখন কিউ এর ফ্রন্টে 10 আছে। 10 কে পপ করি । যেহেতু নোড  10 ভিজিটেড হয়ে গেছে সেহেতু ট্রাভার্সিং প্রক্রিয়া এখানে বন্ধ করি। 

এবার নোড ১ থেকে ১০ পর্যন্ত পাথের দূরত্ব নির্ণয় করি। পাথের দূরত্ব নির্ণয়ের পদ্ধতিটি একদম সহজ। আমরা যে নোডে ভিজিট করব সেই নোডের সাথে প্যারেন্ট নোডের ডিস্টেন্স 1 হবে। যেমন আমরা সর্বশেষ নোড 10 ভিজিট করেছি। নোড 10 থেকে এবার ব্যাক-ট্র্যাকিং করব নোড 1 পর্যন্ত। নোড 10 এর প্যারেন্ট নোড 8; নোড 10 থেকে নোড 8 এর ডিসটেন্স 1 । নোড 8 এর প্যারেন্ট নোড 3; নোড 8 থেকে নোড 3 এর ডিসটেন্স 1 । নোড 3 এর প্যারেন্ট নোড 1; নোড 3 থেকে নোড 1 এর ডিসটেন্স 1 ।  নোড ১ থেকে ১০ পর্যন্ত পাথের সর্বমোট দূরত্ব 3 ।

Code:

/*  BFS */

#include<bits/stdc++.h>
using namespace std;
vector <int> G[100];
bool visit[100]= {0};
int dis[100]={0};
queue <int> q;


int bfs(int s, int d)
{
    int u, v;
    q.push(s);
    visit[s]=1;
    while(!q.empty())
    {
        u=q.front();
        printf("%d ", u);
        q.pop();
        if(u==d)
        {
            return dis[u];
        }
        for(int i=0; i<G[u].size(); i++)
        {
            int v=G[u][i];
            if(visit[v]==0)
            {
                visit[v]=1;
                q.push(v);
                dis[v]=dis[u]+1;
            }
        }
    }
}


int main()
{
    int n, m, u, v, s, d, d1;
    scanf("%d%d", &n, &m);  //n is number of node & m is number of edge
    for(int i=0; i<m; i++)
    {
        scanf("%d%d", &u, &v);  //u and v are two two node of an edge
        G[u].push_back(v);
        G[v].push_back(u); // For bidirectional edge
    }
    printf("S=");
    scanf("%d", &s);
    printf("D=");
    scanf("%d", &d);
    d1=bfs(s, d);
    printf("\n%d", d1);
    return 0;
}

/*
Input:

12 11
1 2
1 3
2 4
2 5
3 6
3 7
3 8
4 9
6 12
8 10
8 11
*/

Adjacency Matrix & Adjacency List

Adjacency Matrix:

অ্যাডজেসেন্ট নোড সম্পর্কে আমরা Graph Theory Introduction এ জেনেছি। একটি নোডের অ্যাডজেসেন্ট নোড হচ্ছে সেই নোডের পাশের নোডগুলো যেগুলো ওই নোডের সাথে এজের মাধ্যমে যুক্ত। এখন আমরা জানবো কিভাবে ম্যাট্রিক্স তৈরি করে বা 2D Array তৈরি করে কোন নোডের অ্যাডজেসেন্ট নোড নির্ণয়ের পদ্ধতি।

উপরে একটি আনডিরেক্টেড গ্রাফ দেয়া আছে। গ্রাফের পাশে একটি টেবিল দেখতে পাচ্ছ। এটি আমাদের অ্যাডজেসেন্সি ম্যাট্রিক্স। ম্যাট্রিক্সের $\left[i\right]\left[j\right]$ ঘরে $1$ দেই  যদি $i$ থেকে $j$ তে কোনো এজ থাকে, না থাকলে $0$ বসিয়ে দেই। গ্রাফটি যদি ডিরেক্টেড গ্রাফ হতো এবং প্রতিটি এজের যদি Weight দেয়া থাকতো তাহলে এমন হতো-

 

এখানে যেহেতু Weight দেয়া আছে সেহেতু এক নোড থেকে অন্য নোডে যেতে যেই কস্ট বা ওয়েইট আছে তা ম্যাট্রিক্সের $\left[i\right]\left[j\right]$ ঘরে বসানো হয়েছে। এক নোড থেকে অন্য নোডে যাওয়া না গেলে সেই ক্ষেত্রে ম্যাট্রিক্সের $\left[i\right]\left[j\right]$ ঘরে ইনফিনিটি value অর্থাৎ Integer বা  Long এর ম্যাক্সিমাম value বসানো হয়েছে। 

অ্যাডজেসেন্সি ম্যাট্রিক্সের সারকথা: সময় ও মেমরির অনেক অপচয় হয় অ্যাডজেসেন্সি ম্যাট্রিক্স ব্যবহার করলে। এটি অ্যাডজেসেন্সি ম্যাট্রিক্সের প্রধান সমস্যা। আবার সুবিধাও আছে- যেমন দুটি নোডের মধ্যে সংযোগ আছে কিনা বা দুটি নোডের এজের কস্ট কত তা খুব সহজেই ম্যাট্রিক্সের [u][v] এর value থেকে জেনে নিতে পারেন।

  

Adjacency List:

উপরের অ্যাডজেসেন্সি ম্যাট্রিক্সকে এবার আমরা অ্যাডজেসেন্সি লিস্টের মধ্যে প্রকাশ করব। 

উপরের গ্রাফ ও ম্যাট্রিক্স লক্ষ্য কর। একটি নোডের সাথে যেসকল নোড যুক্ত আছে সেসকল নোডগুলোকে নিচের নিয়মে লিস্টে সাজাই -

এটিই হচ্ছে উপরের অ্যাডজেসেন্সি ম্যাট্রিক্সের অ্যাডজেসেন্সি লিস্ট। সহজ না ব্যাপারটি ?? এবার এসো এই লিস্টকে কিভাবে প্রোগ্রামিং এর মাধ্যমে ইমপ্লিমেন্ট করবে তা নিয়ে আলোচনা করি। এই লিস্টকে স্টোর দুই ভাবে করতে পারো। Array ব্যবহার করে বা Vector ব্যবহার করে। আমি ভেক্টর ব্যবহার করে কিভাবে অ্যাডজেসেন্সি লিস্ট স্টোর করতে হয় তা জানাবো কারণ Vector, Array এর তুলনায় কম স্পেস অপচয় করে। ভেক্টর ব্যবহার করে অ্যাডজেসেন্সি লিস্ট স্টোর করার আগে STL দিয়ে কিভাবে ভেক্টরে ডাটা রাখা যায় তা এই লিংক থেকে জেনে নাও-STL-Vector Tutorial Link

ভেক্টর দিয়ে অ্যাডজেসেন্সি লিস্ট ইনপুট নেয়ার Code:

#include<bits/stdc++.h>
using namespace std;
int main()
{
    vector <int> G[100];
    int n, m, u, v;
    scanf("%d%d", &n, &m);  //n is number of node & m is number of edge
    for(int i=0; i<m; i++)
    {
        scanf("%d%d", &u, &v);  //u and v are two two node of an edge
        G[u].push_back(v);
        G[v].push_back(u); // For bidirectional edge
    }
    for(int i=0; i<=n; i++)
    {
        for(int j=0; j<G[i].size(); j++)
        {
            printf("%d ",G[i][j]);
        }
        printf("\n");
    }
    return 0;
}